
RTModel
Real-Time Microlensing Modeling
by Valerio Bozza
GD210auw
Binary (too noisy datasets for a good model)
Binary lens models with parallax and orbital motion
 |
Model O1 χ2= 6
1.09367 10 s=0.868828±0.0206619 q=0.179396±0.0396186 u0=0.166121±0.011094 α=1.53879±0.0971681 ρ*=0.0116126±0.00190837 tE=42.4752±5.26756 t0=9287.44±0.432169 πE,N=0.618185±0.323269 πE,E=1.53393±0.370891 (ds/dt)/s=0.00237425±0.000900209 dα/dt=0.000438041±0.00328916 w3=0.00937742±0.00164118 |
 |
Model O2 χ2= 6
1.10384 10 s=0.869234±0.0358281 q=0.192269±0.0387207 u0=-0.167625±0.0217503 α=4.75968±0.0865343 ρ*=0.0120232±0.00165828 tE=42.0521±1.27536 t0=9287.59±0.36937 πE,N=-0.563762±0.314709 πE,E=1.39868±0.257369 (ds/dt)/s=0.00142257±0.00132634 dα/dt=0.00196756±0.00379071 w3=0.00832937±0.00285994 |
Binary lens models with parallax
 |
Model X1 χ2= 6
1.33991 10 s=0.870374±0.0325675 q=0.187204±0.0425133 u0=-0.161172±0.0217621 α=4.59781±0.0939492 ρ*=0.0142644±0.00196193 tE=39.9364±3.79651 t0=9287.12±0.351895 πE,N=-0.912724±0.125199 πE,E=1.71438±0.278625 |
 |
Model X2 χ2= 6
1.36727 10 s=0.872144±0.0121131 q=0.181191±0.0278159 u0=0.161694±0.00579335 α=1.70584±0.0591344 ρ*=0.014365±0.00180155 tE=40.183±3.4907 t0=9287.03±0.158872 πE,N=0.781658±0.069382 πE,E=1.79806±0.262958 |
Binary lens models
 |
Model L1 χ2= 6
2.68742 10 s=0.604337±0.0104853 q=0.384221±0.0294882 u0=0.00391803±0.0137226 α=5.0885±0.0372384 ρ*=0.0115882±0.00196052 tE=44.5562±1.51907 t0=9288.29±0.573755 |
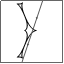 |
Model L2 χ2= 6
3.40787 10 s=0.728033±0.0188883 q=0.412064±0.0960181 u0=0.12991±0.0111953 α=1.2657±0.0872042 ρ*=0.00691479±0.00131708 tE=55.7206±2.42675 t0=9288.9±0.617507 |